给你一个字符串 s，找到 s 中最长的回文子串。
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。示例 2：
输入：s = "cbbd"
输出："bb"提示：
- 1 <= s.length <= 1000
- s 仅由数字和英文字母组成
子串和子序列的区别是，子串一定是连续的，而子序列不一定是连续的。回文子串就是正着看和反着看都一样的子串。比如说字符串 aba 和 abba 都是回文串，因为它们对称，反过来还是和本身一样。
一、暴力破解
用两个变量i和j，判断字符串从i到j的子串是否为回文串，找出最长的回文子串。时间复杂度为 O(n³)，空间复杂度O(1)。
//1.暴力破解
//时间复杂度 O(N^3), 空间复杂度O(1)
public String longestPalindrome(String s) {
char[] charArr = s.toCharArray();
//记录最长回文子串的开始位置和长度
int start = 0, maxLen = 1;
for(int i = 0; i < charArr.length - 1; i++){
for(int j = i + 1; j < charArr.length; j++){
//判断charArr[i,...,j]是否为回文子串，并且是否为最大长度
if(maxLen < j - i + 1 && isPalindrome(charArr,i,j)){
start = i;
maxLen = j - i + 1;
}
}
}
return s.substring(start,start + maxLen);
}
/**
* 验证charArr数组从from到to是否为回文串
*/
public boolean isPalindrome(char[] charArr,int from, int to){
while(from < to){
if(charArr[from] != charArr[to]){
return false;
}
from++;
to--;
}
return true;
}二、动态规划，二维数组: dp[i][j] 表示 s[i, ... ,j] 是否是回文串
动态规划最主要的是dp数组的定义，难点就在于寻找正确的状态转移方程。
1、定义状态
如果s的子串s[i+1,…,j-1]的状态已知，那么我们很容易根据s[i]和s[j]来推出s[i,…,j]的状态，所以定义dp数组dp[i][j]定义为子串s[i,…,j]是否为回文子串，这里是一个boolean变量的二维数组，这里子串定义为左闭右闭区间，即可以取到 s[i] 和 s[j]。
2、状态转移方程
如果s[i] == s[j]，dp[i][j]就取决于dp[i+1][j-1],如果s[i] != s[j]，dp[i][j]就为false，所以状态转移方程如下。
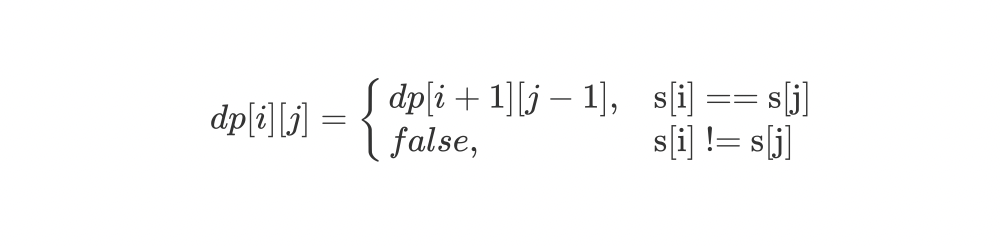
3、边界条件
最基础的情况是只有一个字符，那么它肯定是回文串，也就是在dp数组的对角线上，此时i=j。
如果s[i,…,j]只有2个字符，并且s[i] == s[j]，比如"AA"那么dp[i][j]为true。
如果s[i,…,j]只有3个字符，并且s[i] == s[j]，比如"ABA"那么dp[i][j]为true。
如果i和j位置的元素相同，那么dp[i][j] J就取决于 dp[i+1][j-1]了。
其余情况都为false啦。
4、根据状态转移方程遍历
遍历从左到右从上往下进行，因为s[i,…,j]为s的一个子串，所以 i 小于 j 。初始化我们就把dp对角线的元素都设置为true，也就是一个字符的情况在遍历的时候就不考虑啦。时间复杂度O(n2)，空间复杂度O(n2)。
//2.动态规划
public String longestPalindrome(String s) {
char[] charArr = s.toCharArray();
//dp[i][j] 表示 s[i, ... ,j] 是否是回文串
boolean dp[][] = new boolean[charArr.length][charArr.length];
//dp数组对角线上的表示i=j，即单个字符为回文串
for(int i = 0; i < charArr.length; i++){
dp[i][i] = true;
}
//记录最长回文子串的开始位置和长度
int start = 0, maxLen = 1;
for(int j = 1; j < charArr.length; j++){
for(int i = 0; i < j; i++){
if(charArr[i] == charArr[j]){
//charArr[i,...,j]为两个字符或者三个字符，并且charArr[i] == charArr[j]，那么就是回文子串
if(j - i + 1 == 2 || j - i + 1 == 3){
dp[i][j] = true;
}else{//charArr[i,...,j]大于三个字符，那么取决于charArr[i+1,...,j-1]是否为回文子串
dp[i][j] = dp[i+1][j-1];
}
}else{
dp[i][j] = false;
}
//记录最长回文子串的位置
if(dp[i][j] && maxLen < j - i + 1){
start = i;
maxLen = j - i + 1;
}
}
}
return s.substring(start,start + maxLen);
}三、动态规划，二维数组: dp[i][j]为子串s[i,...,j] 以i开始到j结尾的最大回文子串的长度
如果只用boolean来定义dp二维数组的话，是无法进行状态压缩成一维数组的，如果想把二维数组压缩成一维数组，那么一维数组包含的信息必须做够多。
1、定义状态
dp[i][j]数组的定义，必须能根据s[i+1,…,j-1]的状态推算出s[i,…,j]的状态，我们定义这样一个二维数组， dp[i][j]为子串s[i,...,j] 以i开始到j结尾的最大回文子串的长度，必须以i开头以j结尾。这里子串定义为左闭右闭区间，即可以取到 s[i] 和 s[j]。
2、状态转移方程
如果s[i] == s[j]，并且dp[i+1][j-1]等于s[i+1,...,j-1]的长度，也就是说s[i+1,...,j-1]如果是回文子串的话，在它前面一个位置和后面一个位置分别增加一个相同的元素，那么s[i,...,j]也是回文子串，只需要在原来的长度加上2，这个就是状态转移方程的核心了。如果s[i] != s[j]，必须以i开头以j结尾的回文子串长度就为0，而如果s[i] == s[j]但以i+1开头到j-1结尾的子串不是回文子串，那么s[i+1,...,j-1]两头增加一个相同的元素，它也不是回文子串，因为s[i+1,...,j-1]本身就不是回文子串。所以状态转移方程如下。
3、边界条件
最基础的情况是只有一个字符，那么它肯定是回文串，并且长度为1，也就是在dp数组的对角线上，此时i=j。
分两种情况进行讨论，s[i] == s[j]和s[i] != s[j]。
s[i] == s[j]时：
- 如果
s[i,…,j]只有2个字符，并且s[i] == s[j]，比如"AA"那么dp[i][j]等于2。 - 如果
s[i,…,j]只有3个字符，并且s[i] == s[j]，比如"ABA"那么dp[i][j]等于3。 s[i+1,...,j-1]的长度(j - 1) - (i + 1) + 1=dp[i+1][j-1]，根据状态方程来推算出d[i]p[j]，即dp[i][j] = dp[i+1][j-1] + 2。- 否则
dp[i][j] = 0，因为虽然此时i和j处的元素相等，但s[i+1,…,j-1]并不是回文子串，进而s[i,…,j]也不是回文子串。
s[i] != s[j]时：
- 如果
s[i] != s[j]，那么dp[i][j]=0。
4、根据状态转移方程遍历
遍历从左到右从上往下进行，因为s[i,…,j]为s的一个子串，所以 i 小于 j 。因为初始化我们就把dp对角线的元素都设置为1，也就是一个字符的情况在遍历的时候就不考虑啦。时间复杂度O(n2)，空间复杂度O(n2)。
// 3.动态规划,二维数组: dp[i][j]为子串s[i,...,j] 以i开始到j结尾的最大回文子串的长度
public String longestPalindrome(String s) {
char[] charArr = s.toCharArray();
//dp[i][j]为子串s[i,...,j] 以i开始到j结尾的最大回文子串的长度
int dp[][] = new int[charArr.length][charArr.length];
//dp数组对角线上的表示i=j，即单个字符为回文串，初始化长度为1
for(int i = 0; i < charArr.length; i++){
dp[i][i] = 1;
}
//记录最长回文子串的开始位置和长度
int start = 0, maxLen = 1;
for(int j = 1; j < charArr.length; j++){
for(int i = 0; i < j; i++){
if(charArr[i] == charArr[j]){
//base case：charArr[i,...,j]为两个字符或者三个字符，并且charArr[i] == charArr[j]，那么就是回文子串
if(j - i + 1 == 2 ){
dp[i][j] = 2;
}else if(j - i + 1 == 3){
dp[i][j] = 3;
}else if(dp[i+1][j-1] == (j - 1) - (i + 1) + 1){
//charArr[i,...,j]大于三个字符，那么取决于charArr[i+1,...,j-1]的长度
//如果charArr[i+1,...,j-1]的长度(j - 1) - (i + 1) + 1 = dp[i+1][j-1]，那么charArr[i+1,...,j-1]为回文串，并且charArr[i,...,j]也是回文串
//所以dp[i][j] = dp[i+1][j-1] + 2
dp[i][j] = dp[i+1][j-1] + 2;
}else{
dp[i][j] = 0;
}
}else{
dp[i][j] = 0;
}
//记录最长回文子串的位置
if(dp[i][j] > 0 && maxLen < j - i + 1){
start = i;
maxLen = j - i + 1;
}
}
}
return s.substring(start,start + maxLen);
}四、动态规划，一维数组: dp[j]为子串s[i,...,j] 以j结尾的最大回文子串的长度
方法三的空间复杂度为O(n2)，其实是可以进行状态压缩的，只用一个一维dp数组就可以，前提是进行压缩的二维数组要有足够的信息，才能够压缩成一维数组，如果是方法一的Boolean类型的二维数组就无法进行状态压缩，因为它无法提供足够多的信息。
1、定义状态
dp[j]定义为子串s[i,...,j] 从i开始寻找 以j结尾的最大回文子串的长度，注意dp里面存放的是回文子串的长度了。这里子串定义为左闭右闭区间，即可以取到 s[i] 和 s[j]。
2、状态转移方程
假如s[i+1,...,j-1]为回文子串，并且它的长度为dp[j-1]=(j - 1) - (i + 1) + 1，那么如果s[i] == s[j]，也就有s[i,...,j]也是回文子串，长度增加了2，这个就是状态转移方程的核心了。如果s[i] != s[j]，必须以j结尾的回文子串长度就需要重新计算了，而如果s[i] == s[j]但以i+1开头到j-1结尾的子串不是回文子串，那么必须以j结尾的回文子串长度也需要重新计算。所以状态转移方程如下。
3、边界条件
最基础的情况是第一个字符，它只有自己本身，是回文子串，并且长度为1，所以dp[0]=1。
如果我们知道dp[j-1]，那么从s[j]开始往前推算dp[j-1]个元素来进行最大长度回文子串的感知。
根据dp的定义，我们记子串P=s[j-dp[j-1],...,j-1]为回文子串，那么P前面一个元素的下标为j - dp[j-1] - 1，如果s[j-dp[j-1] - 1] == s[j]，那么s[j-dp[j-1]-1,j-dp[j-1],...,j-1,j]也是回文子串，需要注意下标j - dp[j-1] - 1必须大于零，否则就越界了。
如果s[j-dp[j-1] - 1] != s[j]，此时就没有办法，只能遍历了，但遍历的左边条件可以缩短到j-dp[j - 1]，因为根据dp数组的定义，从下标j-dp[j - 1]再往前不可能构成更长的回文子串了，只需要从s[j-dp[j-1],j-dp[j-1],...,j-1,j]找到一个最长的以j结尾的回文子串即可。
4、根据状态转移方程遍历
遍历从左到右进行，因为s[i,…,j]为s的一个子串，所以 i 小于 j 。时间复杂度O(n2)，空间复杂度O(n)。
// 4.动态规划,一维数组: dp[j]为子串s[i,...,j] 以j结尾的最大回文子串的长度
public String longestPalindrome(String s) {
char[] charArr = s.toCharArray();
//dp[j]为子串s[i,...,j] 以j结尾的最大回文子串的长度
int dp[] = new int[charArr.length];
//第一个字符串为回文串，并且长度为1
dp[0] = 1;
//记录最长回文子串的开始位置和长度
int start = 0, maxLen = 1;
for(int j = 1; j < charArr.length; j++){
if(j - dp[j - 1] - 1 >= 0 && charArr[j] == charArr[j - dp[j - 1] - 1]){
dp[j] = dp[j - 1] + 2;
}else{
//从j - dp[j-1]开始到j进行查找，以j结尾的最长回文子串的长度
int j_len = j - (j - dp[j - 1]) + 1;
for(int i = j - dp[j - 1],right = j;i < j; i++){
if(charArr[i] != charArr[right]){
right = j;
j_len--;
i = j - j_len;
}else{
right--;
}
}
dp[j] = j_len;
}
//记录最长回文子串的位置
if(maxLen < dp[j]){
start = j - dp[j] + 1;
maxLen = dp[j];
}
}
return s.substring(start,start + maxLen);
}五、动态规划，dp使用一维数组: 定义dp[j]表示以位置j结束的最长的回文子串的起始位置
方法四是一种方式使用一维数组来构造动态规划，从而使空间复杂度降低为O(n)。下面我们使用另外一种dp一维数组，也使空间复杂度降低为O(n)。所以说，定义不同的dp数组构造不同的状态转移方程，从而构造不同的动态规划，不过方法都是大同小异的，都很类似，条条大路通罗马，殊途同归而已。
1、定义状态
dp[j]定义为子串s[i,...,j] 以j结尾的最大回文子串的起始位置，注意这是标记的不再是长度了而是回文子串起始点的位置。
2、状态转移方程
上面的方式是根据长度来计算，这次根据起始点的位置计算，也会更容易些。
如果s[i] == s[j]，并且dp[j-1]等于s[i+1,...,j-1]的长度，也就是说s[i+1,...,j-1]如果是回文子串的话，在它前面一个位置和后面一个位置分别增加一个相同的元素，那么s[i,...,j]也是回文子串，唯一不同的是，此时的最长回文子串的起始位置往前移动一个位置，也就是dp[j] = dp[j - 1] - 1，这个就是状态转移方程的核心了。如果s[i] != s[j]，必须以j结尾的最长回文子串的起始位置就需要计算了，只不过不需要从头开始算，因为dp[j-1]记录了j位置前面元素所能感知的范围的开始位置，因此从这个起始位置开始寻找以j结尾的最大回文子串就可以。所以状态转移方程如下。
3、边界条件
最基础的情况是第一个字符，它只有自己本身，是回文子串，并且起始位置为0，所以dp[0]=0。
如果我们知道dp[j-1]，根据dp的定义，我们记子串P=s[dp[j-1],...,j-1]为以j-1结尾的最长回文子串，那么P前面一个元素的下标为dp[j-1] - 1，如果s[dp[j-1] - 1] == s[j]，那么s[dp[j-1]-1,dp[j-1],...,j-1,j]也是回文子串。
如果s[dp[j-1] - 1] != s[j]，此时就没有办法，只能遍历了，但遍历的左边条件可以缩短到dp[j - 1]，因为根据dp数组的定义，从下标dp[j - 1]再往前不可能构成更长的回文子串了，只需要从s[dp[j-1],dp[j-1]+1,...,j-1,j]找到一个最长的以j结尾的最长回文子串即可。
4、根据状态转移方程遍历
遍历从左到右进行，因为s[i,…,j]为s的一个子串，所以 i 小于 j 。时间复杂度O(n2)，空间复杂度O(n)。
// 5.动态规划，dp使用一维数组: 定义dp[j]表示已位置j结束的最长的回文子串的起始位置
public String longestPalindrome5(String s) {
char[] charArr = s.toCharArray();
//定义dp[j]表示已位置j结束的最长的回文子串的起始位置
int dp[] = new int[charArr.length];
//默认第一个元素从0号元素开始，所以初始化为dp[0]初始化为0
dp[0] = 0;
//记录最长回文子串的开始位置和长度
int start = 0, maxLen = 1;
for(int j = 1; j < charArr.length; j++){
//当前位置s[j]等于上一次回文子串左边字符，也就是s[dp[j-1],...,j-1]串左右两边的字符相等
if(dp[j - 1] > 0 && charArr[j] == charArr[dp[j - 1] - 1]){
dp[j] = dp[j - 1] - 1;
}else{
//从dp[j-1]开始到j进行查找，以j结尾的最长回文子串的起始位置
int j_start = dp[j - 1];
for(int i = dp[j - 1],right = j;i < right;i++){
if(charArr[i] != charArr[right]){
right = j;
j_start = i + 1;
}else{
right--;
}
}
dp[j] = j_start;
}
//记录最长回文子串的位置
if(maxLen < j - dp[j] + 1){
start = dp[j];
maxLen = j - dp[j] + 1;
}
}
return s.substring(start,start + maxLen);
}六、中心扩散法
中心扩散的主要思想为，以当前元素为中心，向两边进行扩展，直到找到一个最长的回文子串为止。从中心扩展的时候，考虑从中心一个元素扩展或者从中心两个元素进行扩展，因为回文子串可能是奇数也可能是偶数。时间复杂度O(n2)，空间复杂度O(1)。
//3.中心扩散法
public String longestPalindrome3(String s) {
//记录最长回文子串的开始位置和长度
String palindrome = "";
for(int k = 0; k < s.length(); k++){
String temp = getPalindrome(s,k);
if(palindrome.length() < temp.length()){
palindrome = temp;
}
}
return palindrome;
}
public String getPalindrome(String s, int i){
//寻找以i为中心的回文子串
int from = i, to = i;
while(from >= 0 && to < s.length() && s.charAt(from) == s.charAt(to)){
from--;
to++;
}
String palindrome = s.substring(from + 1,to);
//寻找以 i、i+1 为中心的回文子串
from = i;
to = i + 1;
while(from >= 0 && to < s.length() && s.charAt(from) == s.charAt(to)){
from--;
to++;
}
String palindrome2 = s.substring(from + 1, to);
//返回两个中最长的那个
return palindrome.length() > palindrome2.length()?palindrome:palindrome2;
}七、Manacher算法
1、背景介绍
马拉车算法原名叫Manacher算法，是一位叫Manacher的人发明的。因为谐音的缘故，被国内程序员戏称为马拉车算法。马拉车算法主要用来解决最长回文子串的问题，一般的解法无论是中心探测还是动态规划，时间复杂度都是O(n2)，而马拉车算法可以将时间优化到O(n)。
马拉车算法需要预先对字符串做一些处理，在字符串中插入一些特殊分隔符。本质上此也是基于中心探测法，但中心探测没有考虑到回文的对称性，做了很多无用功。而马拉车 算法在空间上做了很多文章，将之前已经计算过的内容，缓存起来，避免重复的计算，这样就能大幅度提高性能。
首先来回忆下回文串是什么，回文串就是：
- bab
- aba
- 上海自来水来自海上
即正着读、反着读都是一样的字符串。现在给你一个字符串，比如babad，如何求出这个字符串中最长的回文子串呢？这回就要靠马拉车算法了。
2、改进中心探测法
先说下中心探测法，这种方法很好理解，以babad这个字符串为例，中心探测法工作原理如下：
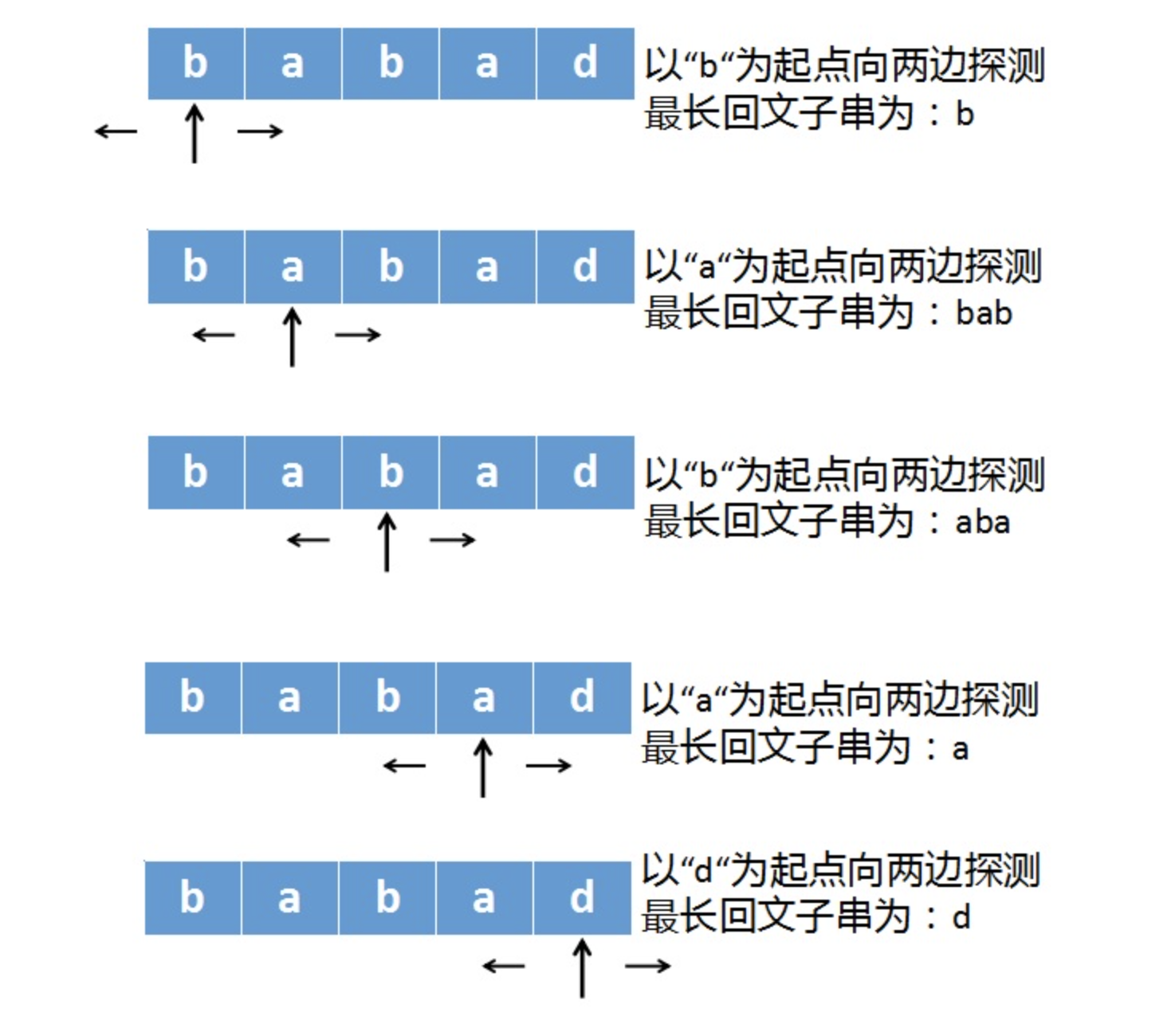
遍历字符串，每遍历到一个字符，就以这个字符为中心，同时往两边扩展，直到两边不等或越界。
根据上述做法，我们就可以求出最长回文串为bab，当时aba也是。
不过上述做法会有个问题，以abb为例，如下图所示：
如果以中心探测来计算，最终会得到最长回文串为a，但实际应该是bb
上述做法错误的原因是，没有考虑到回文串的奇偶长度问题。abbcbba这个字符串长度为7，是以c为中心，两边对称的。而abddbc这个字符串长度为6，是以两个d中间的空隙为中心，两边对称的。回文串的奇偶性质会导致不同的计算方式。计算第二个字符串时，应当将第一个指针指向左边的d，再将第二个指针指向右边的d，第一个指针往左边探测，第二个指针往右边探测，直到两个指针指向的字符不等、或者越界，如下图所示：
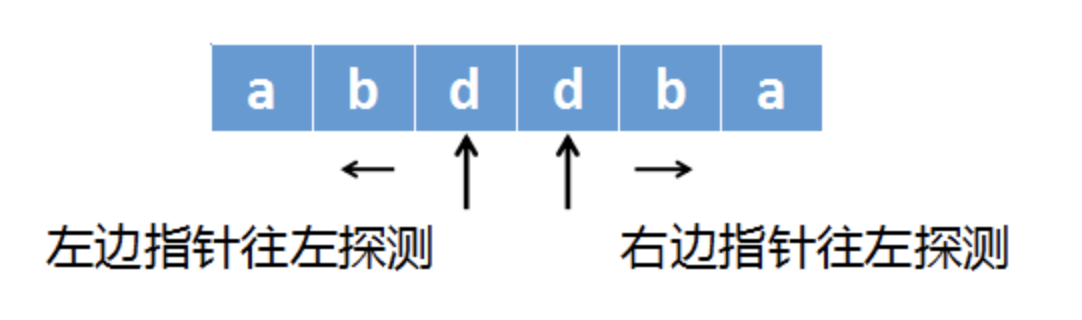
由于我们并不知道最长回文子串到底是奇数长度、还是偶数长度。
所以在计算的时候，需要将奇数和偶数的情况都计算一次，再求一个最大值。
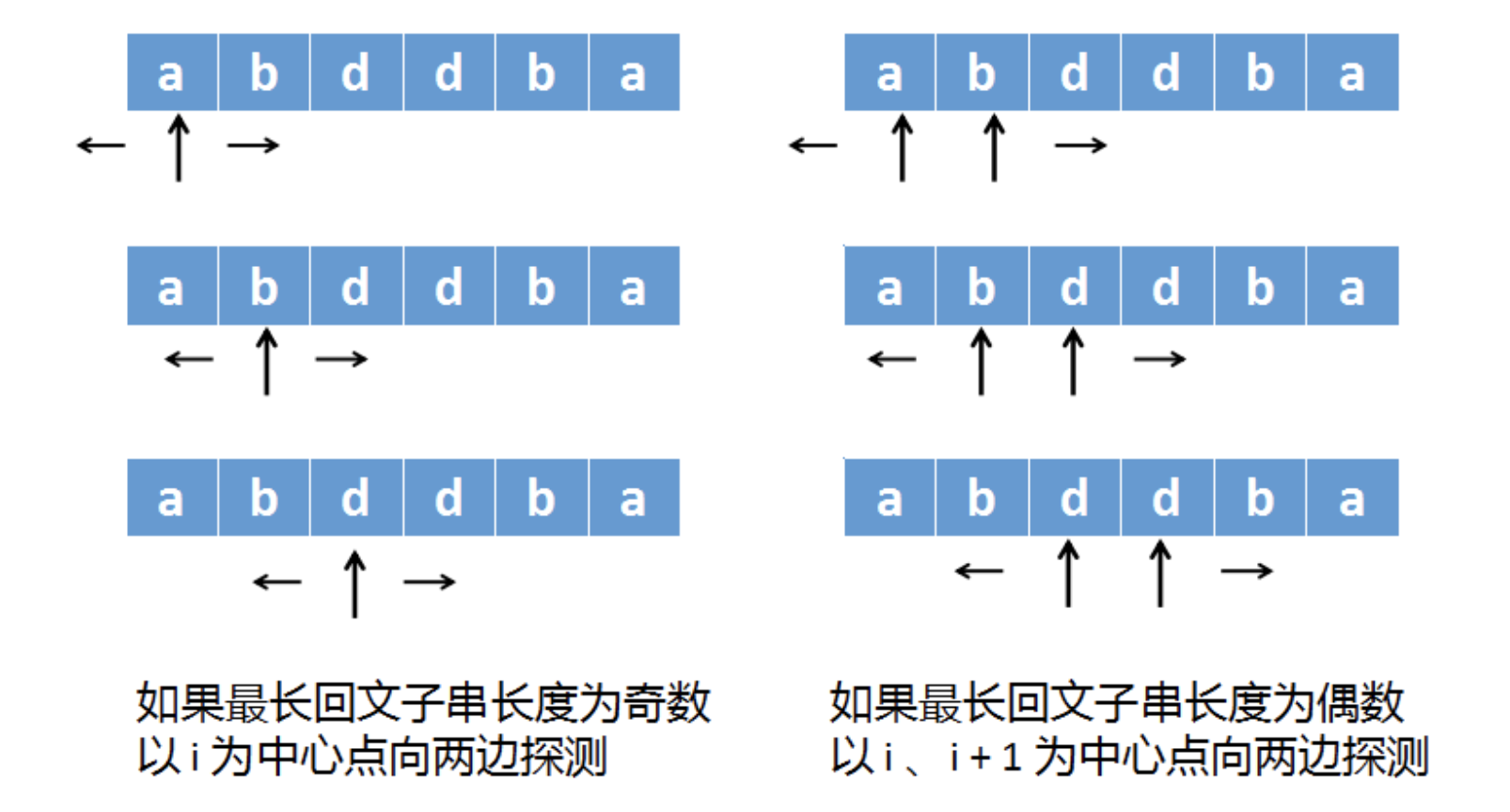
现在我们对原始字符串做一些处理，来解决子串奇偶长度问题，如下图：
之后我们就可以忽略奇偶长度问题，统一的用中心探测法来求最长回文子串，假设原始字符串为xabbcbbay，经过处理后如下图：
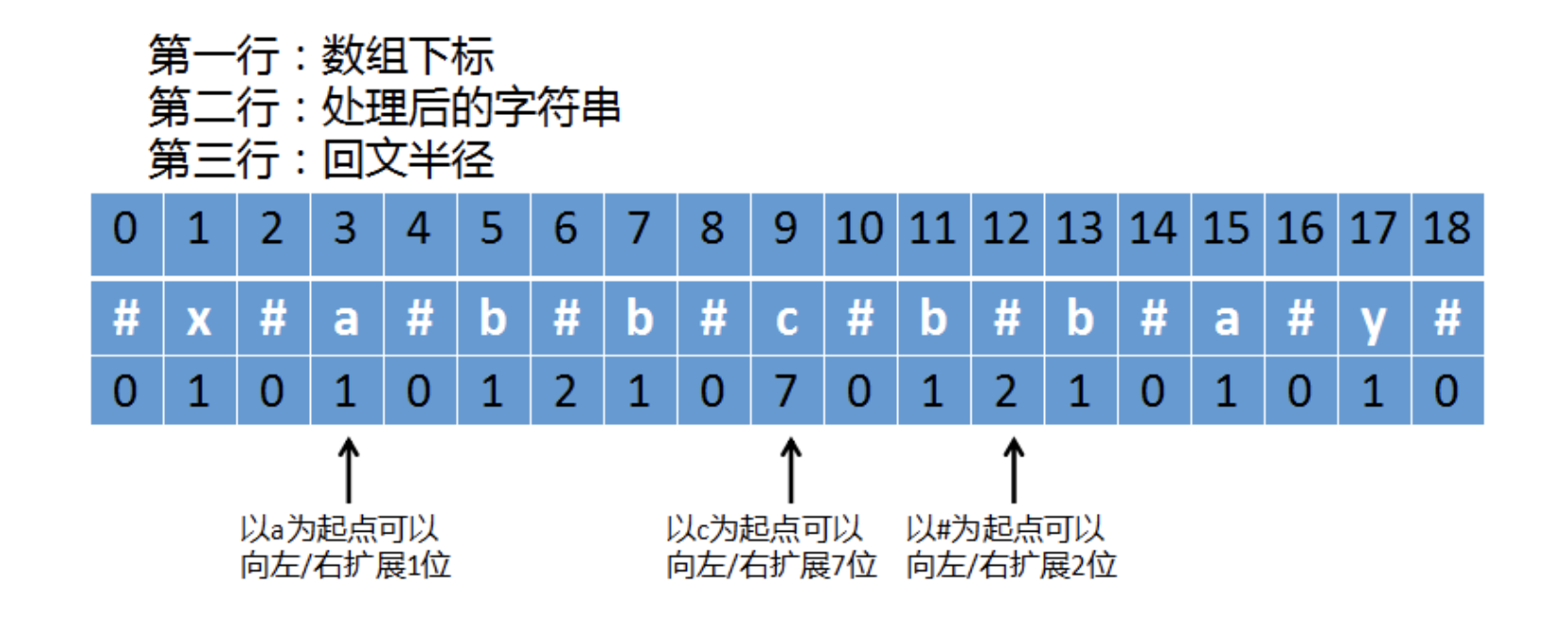
上图中，最重要的是第三行，即回文半径，
- 最左边的箭头上指向的
a这个字符，它可以向左/向右扩展1位，也就是变成#a#这样的回文串，这个字符串总长度是3，以a为中心可以向两边扩展1位(不包括a字符本身)，所以这个字符的回文半径是1。 - 中间箭头指向的
c这个字符，它可以向左/向右扩展7位，即往左是:#a#b#b#，往右是#b#b#a#，以c为中心可以向两边扩展7位(不包括c字符本身)，所以这个字符的回文半径是7。 - 最右边箭头指向的
#这个字符，它可以向左/向右扩展2位，也就是变成#b#b#这样的回文串，这个字符串总长度是5，以#为中心可以向两边扩展2位，所以这个字符的回文半径是2。
好，重点来了。
原始字符是xabbcbbay，它的长度为9。而经过处理后的字符串#x#a#b#b#c#b#b#a#y#，它的长度为19，也就是说 *原字符串长度 2 + 1 就等于 处理后的字符串长度。现在计算回文半径**时，这个长度不包括箭头指向的字符本身。
那么计算出来的回文半径最大值，就等于原始字符串中最长回文串的长度，即上图中间那个箭头指向的字符c其回文半径长度为7(对应的数组下标是9)，而原始字符串中最长回文串为abbcbba，其长度也是7。于是我们遍历处理后的字符串，当遍历到下标9时，就会得到计算出最长回文半径7，我们通过下标和回文半径就可以更新start(原始字符最长回文串的起始位置)：
i:当前遍历到的数组下标
armLen:以i为中心，计算出的回文半径
start = (i - armLen) / 2
maxLen = armLen
等字符串全部遍历完，我们根据start和maxLen这两个变量，就可以从原始字符串s中截取出最长回文子串：
s[start : start + maxLen]
我们用#作为分隔符，如果原始字符串中包含了这个字符怎么办呢？没关系，分隔符可以用任意字符，甚至跟原始字符串中的某个字符重复也可以的，因为我们只是要计算出某个字符的回文半径，并不需要分隔符本身。由于每遍到一个字符，都需要往左/右进行探测，故这种方式的时间复杂度是O(n2)空间复杂度是O(1)。效率仍然是不高，但是已有有马拉车算法的基本雏形了，后面就是在此基础上做优化，增加辅助空间来优化时间。
代码实现：
class Solution {
public String longestPalindrome(String s) {
if(s==null || s.length() == 0) {
return "";
}
//对原始字符串做处理，将abc变成#a#b#c#
StringBuilder tmp = new StringBuilder();
tmp.append("#");
for(int i = 0; i < s.length(); ++i) {
tmp.append("#");
tmp.append(s.charAt(i));
}
tmp.append("#");
int start = 0;
int maxLen = 0;
int n = tmp.length();
//从左到右遍历处理过的字符串，求每个字符的回文半径
for(int i = 0; i < n; ++i) {
//计算当前以i 为中心的回文半径
int cur = expand(tmp, i, i);
//如果当前计算的半径大于maxLen，就更新start(原始字符的起始位置)
if(cur > maxLen) {
start = (i - cur) / 2;
maxLen = cur;
}
}
//根据start和maxLen，从原始字符串中截取一段返回
return s.substring(start, start + maxLen);
}
//以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
//所以在返回的总长度时要减去2
private int expand(StringBuilder s, int left, int right) {
while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
--left;
++right;
}
return (right - left - 2) / 2;
}
}
3、马拉车算法
上面的代码在计算过程中，没有用到辅助空间，计算#x#a#b#b#c#b#b#a#y#中每个字符的回文半径时，都需要往两边扩展一点点计算。实际上，我们可以将之前计算过的回文半径保存到一个数组中，后面再计算某个字符的回文半径时，就可以利用到之前已经计算过的值。
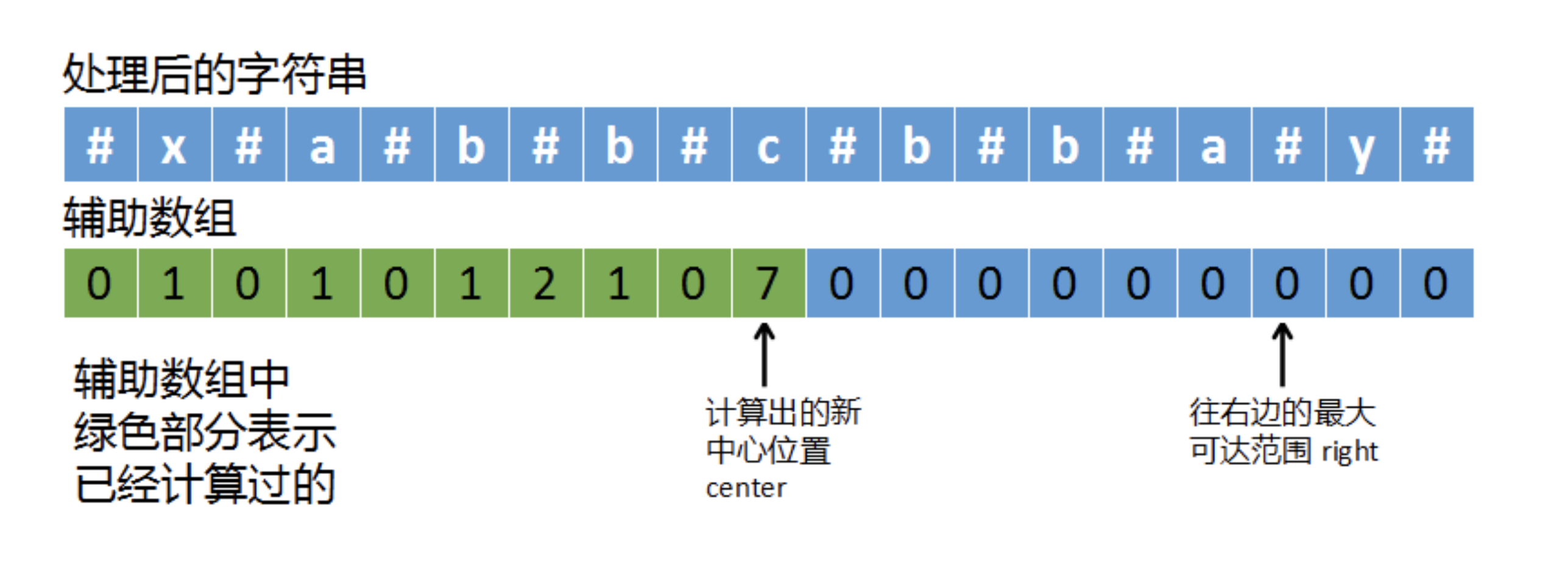如上图，我们需要两个辅助变量：
- right，表示已经探测到的字符串最右边的可达范围
- center，根据最右边的可达范围的中心对称位置
因为我们是从左往右遍历字符串的，比如当我们计算c这个字符时，可以得知它的回文半径是7，那么就以c为中心点，向右扩展7位，这个位置就是right指向的位置(对应上图中最右边的箭头)。
right这个位置，就是我们目前已经计算出的最右端可达范围，以right和中心对称位置center得到的回文串不一定是最长的，但是right是目前我们能探测到的最远的右端位置。我们在遍历字符串的同时，也在不断扩大right的范围，right和它的左边都是已经探测过的，right的右边是未探测的。
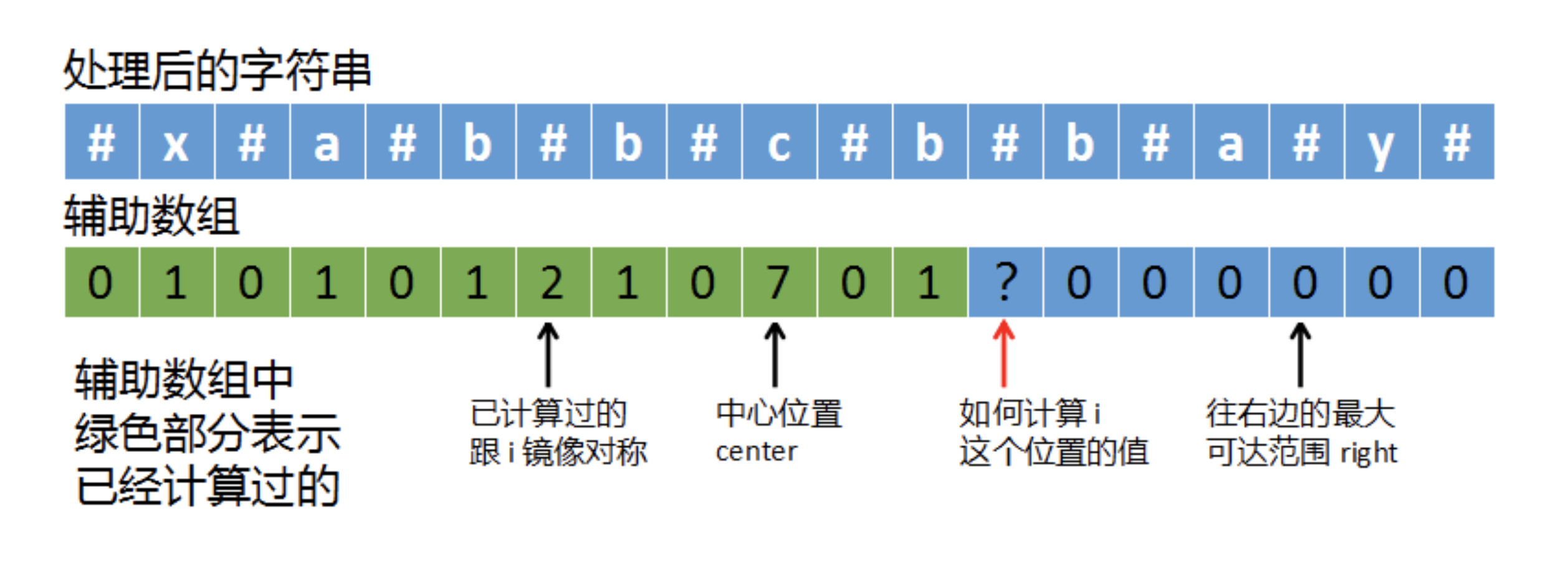
上图中，红色箭头指向了#字符，如果用中心探测法计算这个字符的回文半径，我们就得不断往左/右边进行扩展，直到左右字符不等或者越界。由于是从左往右遍历的，center和right的位置也是根据i来推动的，所以i肯定是大于等于center的。而回文的特点是左右对称，根据中心位置center，我们就可以找到i的镜像位置，也就是上图中最左边箭头指向的i镜像对称(i_mirror)。实际上i镜像的值是已经计算过的，它的回文半径是2，那么我们可以根据已知的i镜像的值来计算出i的值。因为i和i_mirror是根据center对称的，故i + i_mirror = 2 * center，于是可以得到i镜像的下标为：
i_mirror = 2 * center - i
假定数组p中保存了已计算过的回文半径值，那么p[i_mirror]就是i以center为中心镜像对称位置的回文半径长度。根据数组p[i_mirror]来计算p[i]又分两种情况：
- right < i
- right >= i
第一种情况right < i，说明要计算的i超过了right的范围，如下如所示：
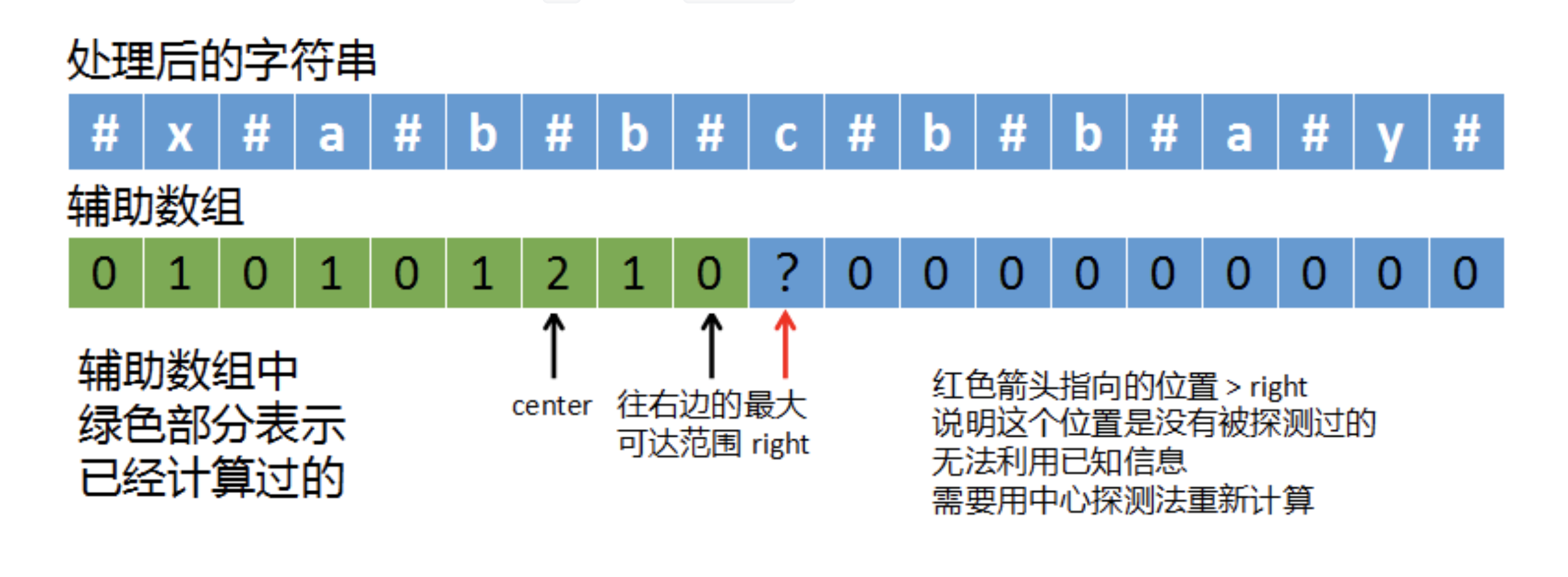
这种情况下，由于i所指向的字符落在right范围之外，说明这个字符没有被探测过，这样的话，就不能再利用已有的信息了，只能用中心探测法，一点一点的向外扩展计算。
第二种情况right >= i，又分细分成三种小情况。
(1)、如果right - i > p[i_mirror]
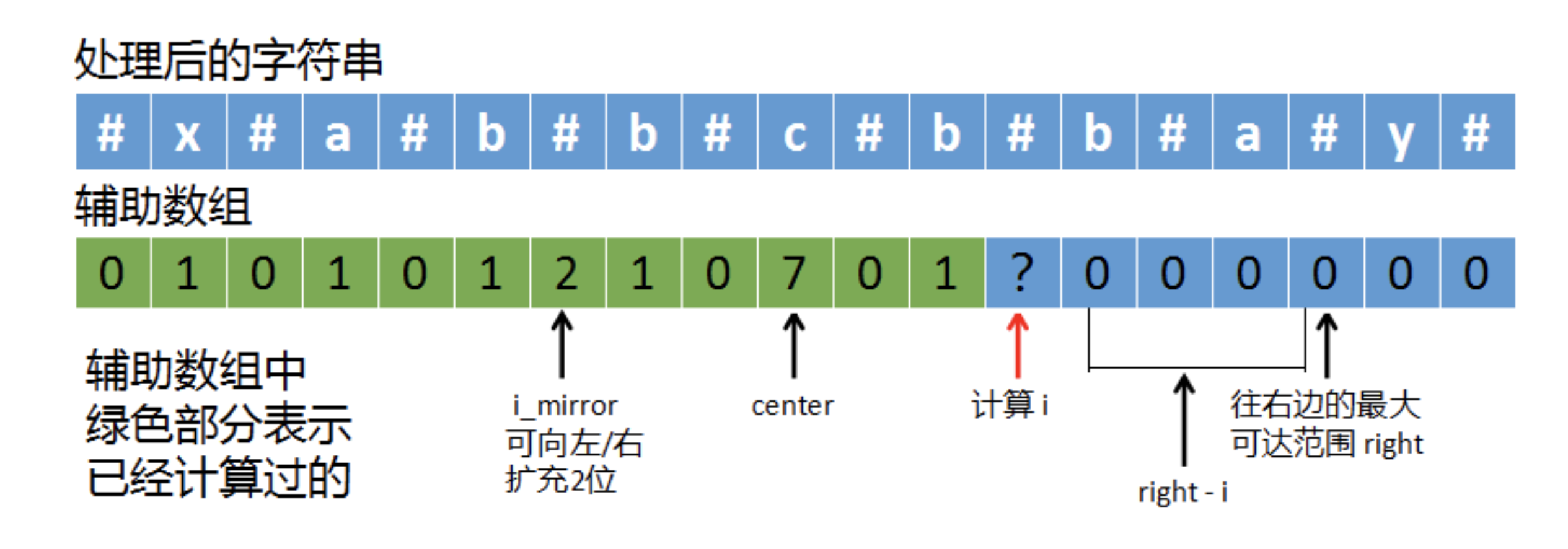
如上图，p[i_mirror]为2，它表示以i_mirror为中心可以向左/右扩展2位。right - i为4，它表示从i的位置到已探测的最右端right距离为4。在计算i时，我们可以选择扩展2位，因为i_mirror和i是镜像对称的，p[i_mirror]可以扩展两位，那么i也有可能扩展2位。也可以选择扩展4位，i到right的距离是4，由right是已探测的最右端位置，那么i-right这段，理论上来说也有可能是回文，所以也有可能扩展4位。但我们需要选择一个保守的，从上图中也可以发现，如果选择4就不对了，所以当right - i和p[i_mirror]不同时，我们选择较小的那个值。
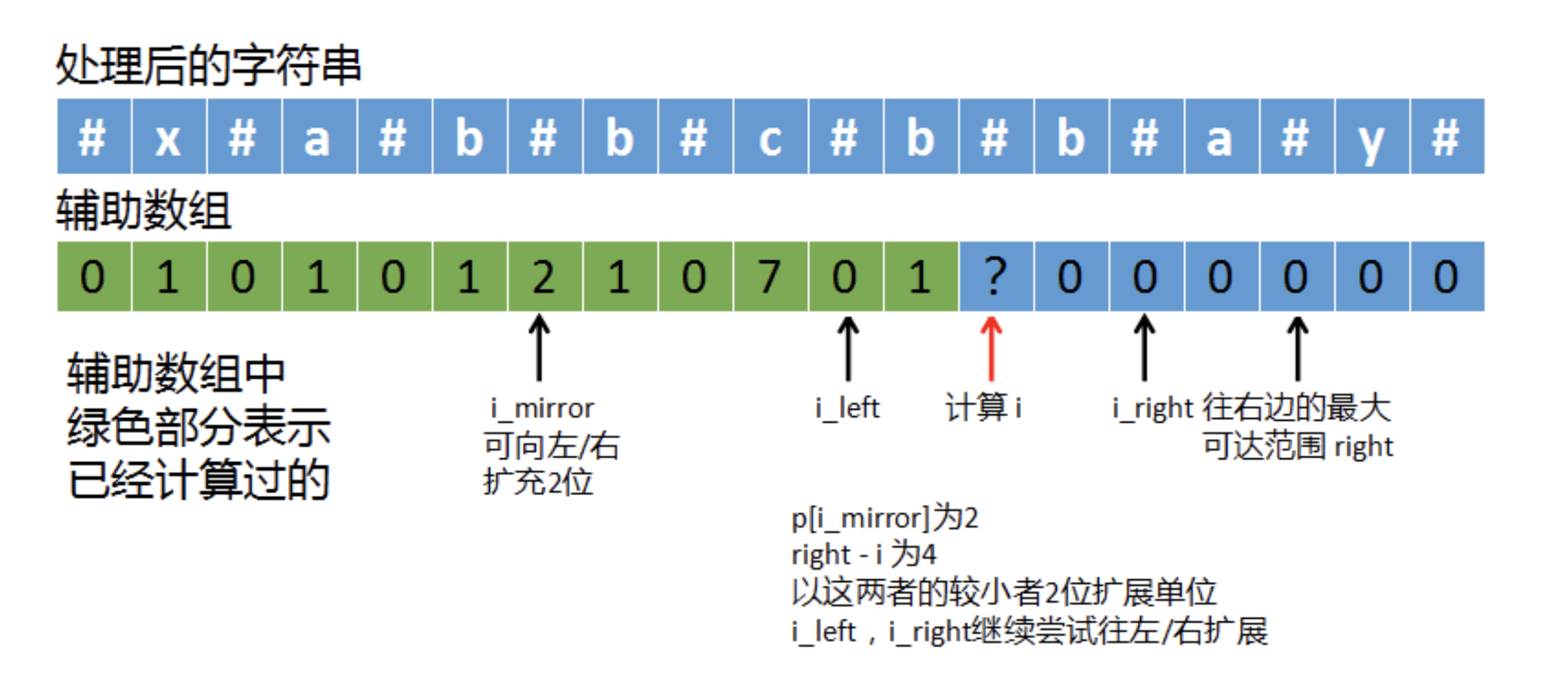
如上图，这次我们在计算i的时候，就不用像中心探测法那样，以i为中心向两边探测了，而是计算出两个新起点i_left和i_right。i_left就等于i - 2，i_right等于i + 2，这里的2就是p[i_mirror]的值。我们让i_left和i_right一个往左、一个往右开始探测，这等于是跳过了一些检查的位置，这就是马拉车算法的关键所在，利用已知的i_mirror信息来扩展i，跳过一些已经确定的位置，省去了多余的判断。
(2)、如果right - i == p[i_mirror]
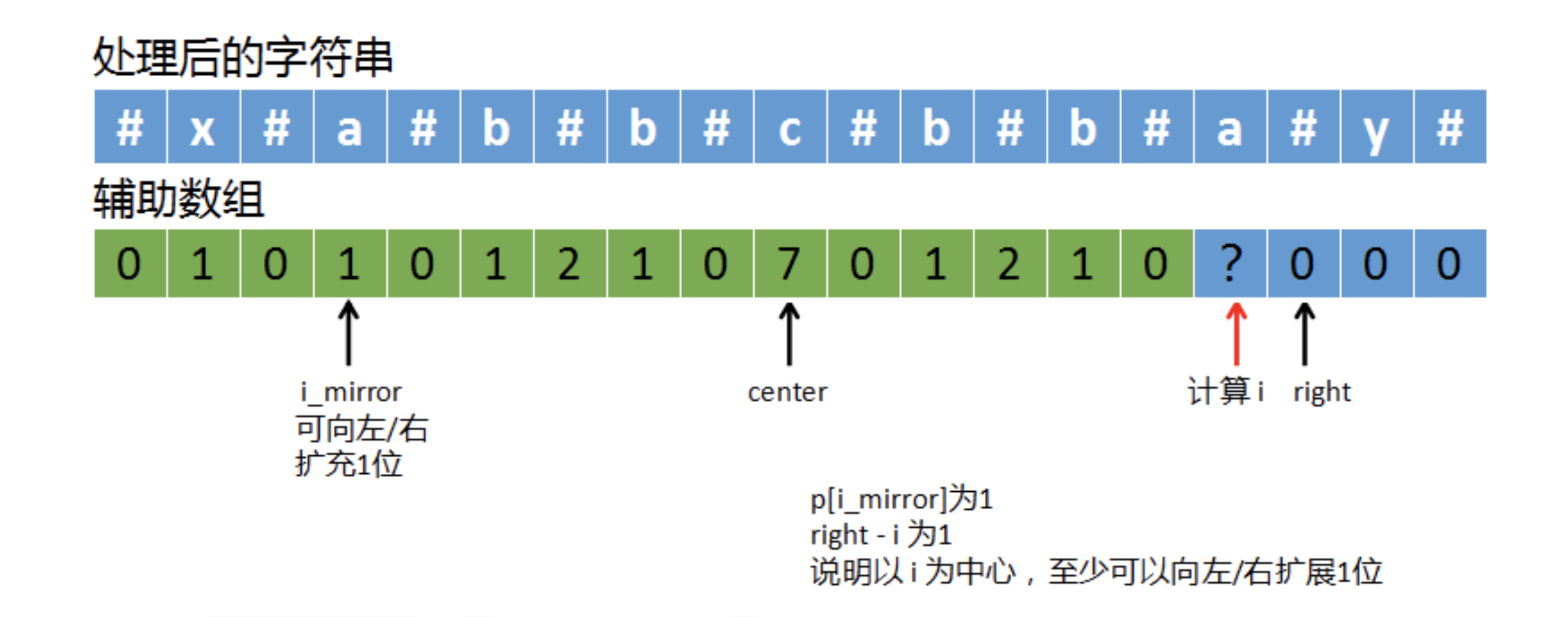
如上图，p[i_mirror]为1，right - i也是为1。这就说明以i为中心至少可以再向左/右扩展1位。我们让i_left = i + 1，让i_right = i + 1，然后以i_left和i_right为新起点，继续往左/右扩展。
(3)如果right - i < p[i_mirror]
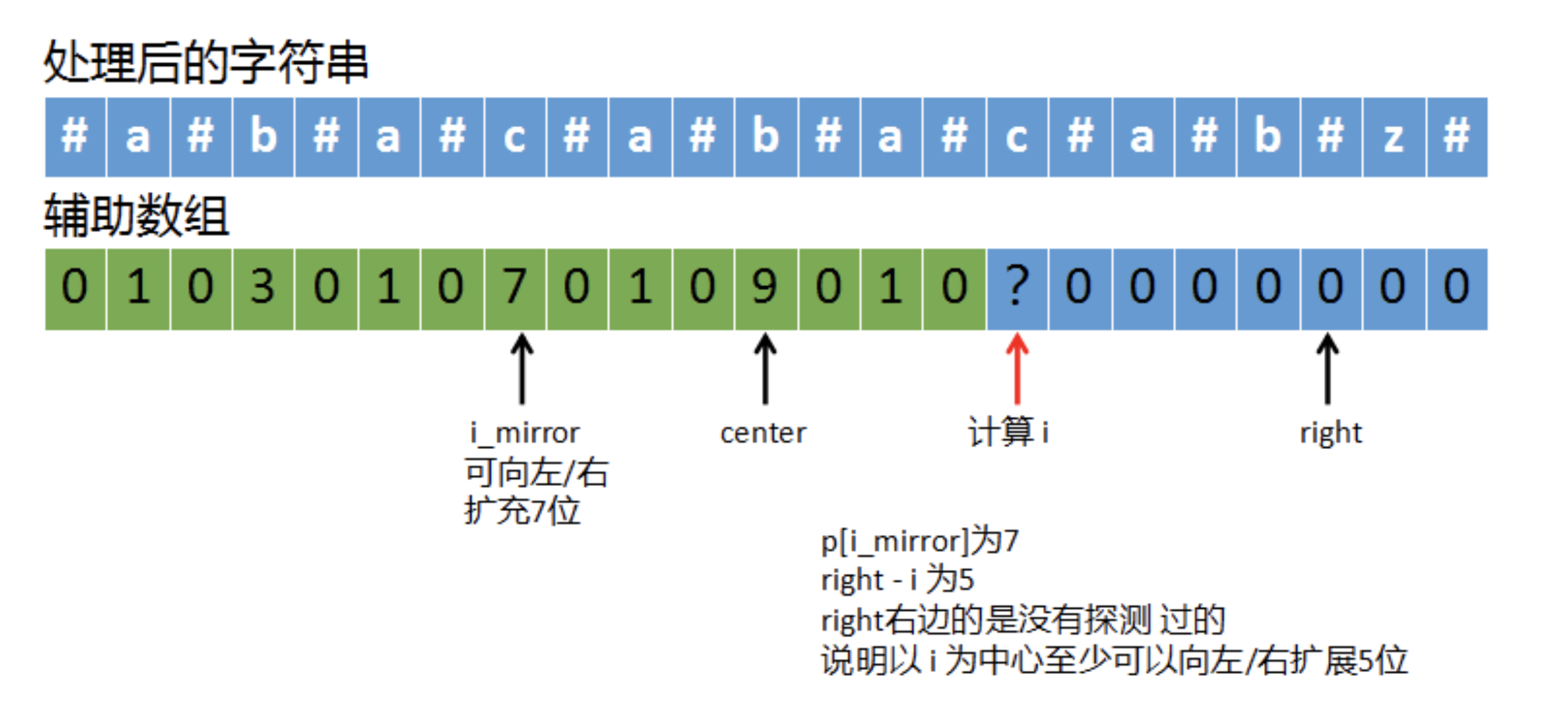
如上图，我们要计算i，此时p[i_mirror]为7，也就是i的镜像位置是可以向左/右扩展7的，但是i可能不行，因为right - i为5，right是我们已经考察过的最右端的位置，i是否可以扩展到right右边我们并不清楚，但是可以肯定是是，至少我们可以向左/右扩展5位，也就是选择right - i和p[i_mirror]中较小的5来扩展。
综上(1)、(2)、(3)我们计算i的回文半径方式如下：
i_mirror = 2 * center - i
最小扩展单位 = min(right - i, p[i_mirror])
以i为中心的回文半径 = expand(i - 最小扩展单位, i + 最小扩展单位)
马拉车算法仍然是外面一个for循环，里面再套了一个while循环。但对于每个位置i，扩展要么从当前的最右端的right开始，要么只会进行一步，而right最多向前走N，故时间复杂度为O(n)，空间复杂度为O(n)。
代码实现：
//4.Manacher算法
public String longestPalindrome4(String s) {
if(null == s || s.length() == 0){
return "";
}
//对原始字符串做处理，将abc变成#a#b#c#
StringBuilder tmp = new StringBuilder();
for(int i = 0; i < s.length(); ++i) {
tmp.append("#");
tmp.append(s.charAt(i));
}
tmp.append("#");
int n = tmp.length();
//right表示目前计算出的最右端范围，right和左边都是已探测过的
int right = 0;
//center最右端位置的中心对称点
int center = 0;
int start = 0;
int maxLen = 0;
//p数组记录所有已探测过的回文半径，后面我们再计算i时，根据p[i_mirror]计算i
int[] p = new int[n];
//从左到右遍历处理过的字符串，求每个字符的回文半径
for(int i = 0; i < n; ++i) {
//根据i和right的位置分为两种情况：
//1、i<=right利用已知的信息来计算i
//2、i>right，说明i的位置时未探测过的，只能用中心探测法
if(right >= i) {
//这句是关键，不用再像中心探测那样，一点点的往左/右扩散，根据已知信息
//减少不必要的探测，必须选择两者中的较小者作为左右探测起点
int minArmLen = Math.min(right - i, p[2 * center - i]);
p[i] = expand(tmp, i - minArmLen, i + minArmLen);
}
else {
//i落在right右边，是没被探测过的，只能用中心探测法
p[i] = expand(tmp, i, i);
}
//大于right，说明可以更新最右端范围了，同时更新center
if(i + p[i] > right) {
center = i;
right = i + p[i];
}
//找到了一个更长的回文半径，更新原始字符串的start位置
if(p[i] > maxLen) {
start = (i - p[i]) / 2;
maxLen = p[i];
}
}
//根据start和maxLen，从原始字符串中截取一段返回
return s.substring(start, start + maxLen);
}
//以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
//所以在返回的总长度时要减去2
private int expand(StringBuilder s, int left, int right) {
while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
--left;
++right;
}
return (right - left - 2) / 2;
}
加油，小景哥哥，你是最棒的