各种经典排序算法详解
①排序的分类
按照存储介质来分,可以分为内部排序和外部排序。
- 内部排序:数据一直在内存中进行的排序称为内部排序。
- 外部排序:当数据量很大时无法全部拷贝到内存需要使用外存的时候,称为外部排序。
按照排序的特点来分,内部排序包括比较排序和非比较排序。
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
比较排序包括插入/选择/交换/归并排序,非比较排序包括计数/基数/桶排序。插入排序包括直接插入/希尔排序,选择排序包括直接选择/堆排序,交换排序包括冒泡/快速排序。
按照数据排序的稳定性来分,可以分为稳定排序和不稳定排序。
- 稳定:如果数据m和n相等,排序前m在n的前面,排序后m仍在n的前面,则称为稳定排序。
- 不稳定:如果数据m和n相等,排序前m在n的前面,排序后m可能会出现在 n的后面,则称为不稳定排序。

②各排序算法时间复杂度对比
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | 内部排序 | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 内部排序 | 不稳定 |
| 插入排序 | O(n2) | O(n) | O(n2) | O(1) | 内部排序 | 稳定 |
| 希尔排序 | O(n log n) | O(n log2n) | O(n log2n) | O(1) | 内部排序 | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 外部排序 | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | O(n log n) | 内部排序 | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 内部排序 | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | 外部排序 | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n2) | O(n+k) | 外部排序 | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 外部排序 | 稳定 |
其中,n表示数据的数量,k表示数据的位数。
③排序算法思想
冒泡排序(Bubble Sort)的原理
比较相邻的元素,如果第一个比第二个大就进行交换,对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,每一轮排序后末尾元素都是有序的,这样元素越大的元素就会经由交换慢慢“沉”到数据的尾端,并且排序的无序数据每次减少一个(末尾有序的一个),针对 n 个元素重复以上步骤 n – 1 次排序完毕。
public void bubbleSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
for (int index = 0; index < nums.length - 1 - i; index++) {
if (nums[index] > nums[index + 1]){
swap(nums, index, index + 1);
}
}
}
}当序列已经有序时仍会进行不必要的比较,可以设置一个标志记录是否有元素交换,如果没有直接结束比较。
public void betterBubbleSort(int[] nums) {
boolean swap;
for (int i = 0; i < nums.length - 1; i++) {
swap = true;
for (int index = 0; index < nums.length - 1 - i; index++) {
if (nums[index] > nums[index + 1]) {
swap(nums, index ,index + 1);
swap = false;
}
}
if (swap) break;
}
}动图演示
选择排序(Selection Sort)的原理
每次在未排序序列中找到最小元素,和未排序序列的第一个元素交换位置,再在剩余未排序序列中重复该操作直到所有元素排序完毕。
public void selectSort(int[] nums) {
int minIndex;
for (int index = 0; index < nums.length - 1; index++){
minIndex = index;
for (int i = index + 1;i < nums.length; i++){
if(nums[i] < nums[minIndex])
minIndex = i;
}
if (index != minIndex){
swap(nums, index, minIndex);
}
}
}动图演示
插入排序(Insertion Sort)的原理
每一趟将一个待排序记录按其关键字的大小插入到已排好序的一组记录的适当位置上,直到所有待排序记录全部插入为止。
public void insertionSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int insertNum = nums[i];
int insertIndex;
for (insertIndex = i - 1; insertIndex >= 0 && nums[insertIndex] > insertNum; insertIndex--) {
nums[insertIndex + 1] = nums[insertIndex];
}
nums[insertIndex + 1] = insertNum;
}
}直接插入没有利用到要插入的序列已有序的特点,插入第 i 个元素时可以通过二分查找找到插入位置 insertIndex,再把 i~insertIndex 之间的所有元素后移一位,把第 i 个元素放在插入位置上。
public void binaryInsertionSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int insertNum = nums[i];
int insertIndex = -1;
int start = 0;
int end = i - 1;
while (start <= end) {
int mid = start + (end - start) / 2;
if (insertNum > nums[mid])
start = mid + 1;
else if (insertNum < nums[mid])
end = mid - 1;
else {
insertIndex = mid + 1;
break;
}
}
if (insertIndex == -1)
insertIndex = start;
if (i - insertIndex >= 0)
System.arraycopy(nums, insertIndex, nums, insertIndex + 1, i - insertIndex);
nums[insertIndex] = insertNum;
}
}动图演示
希尔排序(Shell Sort)的原理
又称缩小增量排序,是对直接插入排序的改进,把记录按下标的一定增量分组,对每组进行直接插入排序,每次排序后减小增量,当增量减至 1 时排序完毕。
public void shellSort(int[] nums) {
for (int d = nums.length / 2; d > 0 ; d /= 2) {
for (int i = d; i < nums.length; i++) {
int insertNum = nums[i];
int insertIndex;
for (insertIndex = i - d; insertIndex >= 0 && nums[insertIndex] > insertNum; insertIndex -= d) {
nums[insertIndex + d] = nums[insertIndex];
}
nums[insertIndex + d] = insertNum;
}
}
}动图演示
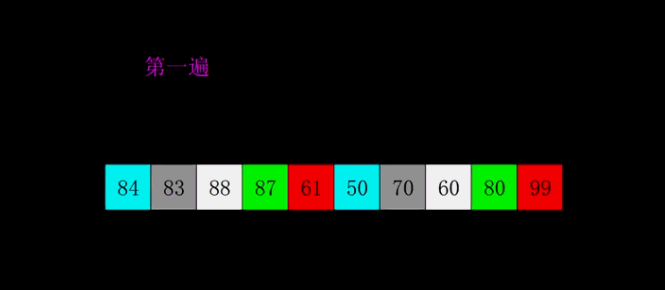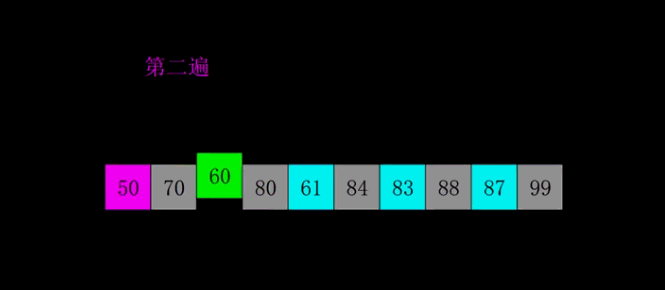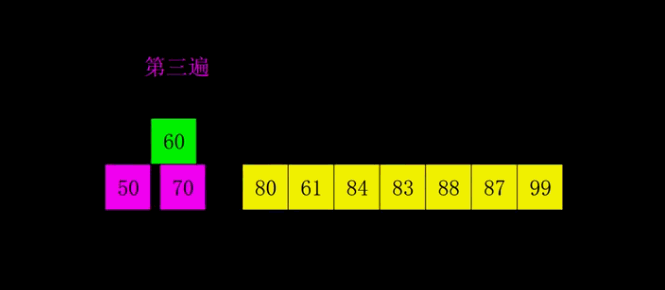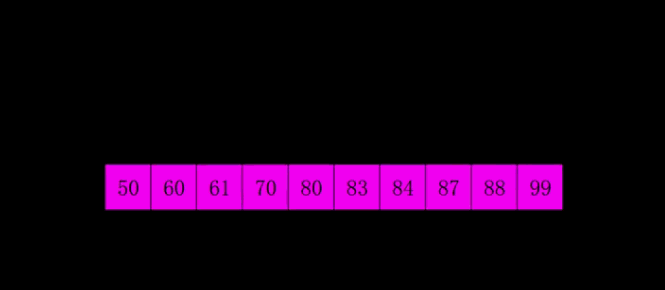
归并排序(Merge Sort)的原理
归并排序基于归并操作,是一种稳定的排序算法。
基本原理:应用分治法将待排序序列分成两部分,然后对两部分分别递归排序,最后进行合并,使用一个辅助空间并设定两个指针分别指向两个有序序列的起始元素,将指针对应的较小元素添加到辅助空间,重复该步骤到某一序列到达末尾,然后将另一序列剩余元素合并到辅助空间末尾。
适用场景:数据量大且对稳定性有要求的情况。
public void mergeSort(int[] arr) {
int[] help = new int[arr.length];
sort(arr, 0, arr.length - 1);
}
public void sort(int[] arr, int start, int end) {
if (start == end) return;
int mid = start + (end - start) / 2;
sort(arr, start, mid);
sort(arr, mid + 1, end);
merge(arr, start, mid, end);
}
public void merge(int[] arr, int start, int mid, int end) {
if (end + 1 - start >= 0) System.arraycopy(arr, start, help, start, end + 1 - start);
int p = start;
int q = mid + 1;
int index = start;
while (p <= mid && q <= end) {
if (help[p] < help[q])
arr[index++] = help[p++];
else
arr[index++] = help[q++];
}
while (p <= mid) arr[index++] = help[p++];
while (q <= end) arr[index++] = help[q++];
}动图演示
快速排序(Quick Sort)的原理
是对冒泡排序的一种改进,不稳定,平均/最好时间复杂度 O(nlogn),元素基本有序时最坏时间复杂度 O(n²),空间复杂度 O(logn)。
首先选择一个基准元素,通过一趟排序将要排序的数据分割成独立的两部分,一部分全部小于等于基准元素,一部分全部大于等于基准元素,再按此方法递归对这两部分数据进行快速排序。
快速排序的一次划分从两头交替搜索,直到 low 和 high 指针重合,一趟时间复杂度 O(n),整个算法的时间复杂度与划分趟数有关。
最好情况是每次划分选择的中间数恰好将当前序列等分,经过 log(n) 趟划分便可得到长度为 1 的子表,这样时间复杂度 O(nlogn)。
最坏情况是每次所选中间数是当前序列中的最大或最小元素,这使每次划分所得子表其中一个为空表 ,这样长度为 n 的数据表需要 n 趟划分,整个排序时间复杂度 O(n²)。
public void quickSort(int[] nums, int start, int end) {
if (start < end) {
int pivotIndex = getPivotIndex(nums, start, end);
quickSort(nums, start, pivotIndex - 1);
quickSort(nums, pivotIndex + 1, end);
}
}
public int getPivotIndex(int[] nums, int start, int end) {
int pivot = nums[start];
int low = start;
int high = end;
while (low < high) {
while (low <= high && nums[low] <= pivot)
low++;
while (low <= high && nums[high] > pivot)
high--;
if (low < high)
swap(nums, low, high);
}
swap(nums, start, high);
return high;
}优化:当规模足够小时,例如 end - start < 10 时,采用直接插入排序。
动图演示
堆排序(Heap Sort)的原理
是对直接选择排序的改进,不稳定,时间复杂度 O(nlogn),空间复杂度 O(1)。
将待排序记录看作完全二叉树,可以建立大根堆或小根堆,大根堆中每个节点的值都不小于它的子节点值,小根堆中每个节点的值都不大于它的子节点值。
以大根堆为例,在建堆时首先将最后一个节点作为当前节点,如果当前节点存在父节点且值大于父节点,就将当前节点和父节点交换。在移除时首先暂存根节点的值,然后用最后一个节点代替根节点并作为当前节点,如果当前节点存在子节点且值小于子节点,就将其与值较大的子节点进行交换,调整完堆后返回暂存的值。
public void add(int[] nums, int i, int num){
nums[i] = num;
int curIndex = i;
while (curIndex > 0) {
int parentIndex = (curIndex - 1) / 2;
if (nums[parentIndex] < nums[curIndex])
swap(nums, parentIndex, curIndex);
else break;
curIndex = parentIndex;
}
}
public int remove(int[] nums, int size){
int result = nums[0];
nums[0] = nums[size - 1];
int curIndex = 0;
while (true) {
int leftIndex = curIndex * 2 + 1;
int rightIndex = curIndex * 2 + 2;
if (leftIndex >= size) break;
int maxIndex = leftIndex;
if (rightIndex < size && nums[maxIndex] < nums[rightIndex])
maxIndex = rightIndex;
if (nums[curIndex] < nums[maxIndex])
swap(nums, curIndex, maxIndex);
else break;
curIndex = maxIndex;
}
return result;
}动图演示

计数排序(Counting Sort)的原理
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法描述:
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
public void countingSort(int[] nums, maxValue) {
int[] bucket = new int(maxValue + 1);
int sortedIndex = 0;
int arrLen = nums.length,
int bucketLen = maxValue + 1;
for (int i = 0; i < arrLen; i++) {
if (!bucket[nums[i]]) {
bucket[nums[i]] = 0;
}
bucket[nums[i]]++;
}
for (int j = 0; j < bucketLen; j++) {
while(bucket[j] > 0) {
nums[sortedIndex++] = j;
bucket[j]--;
}
}
}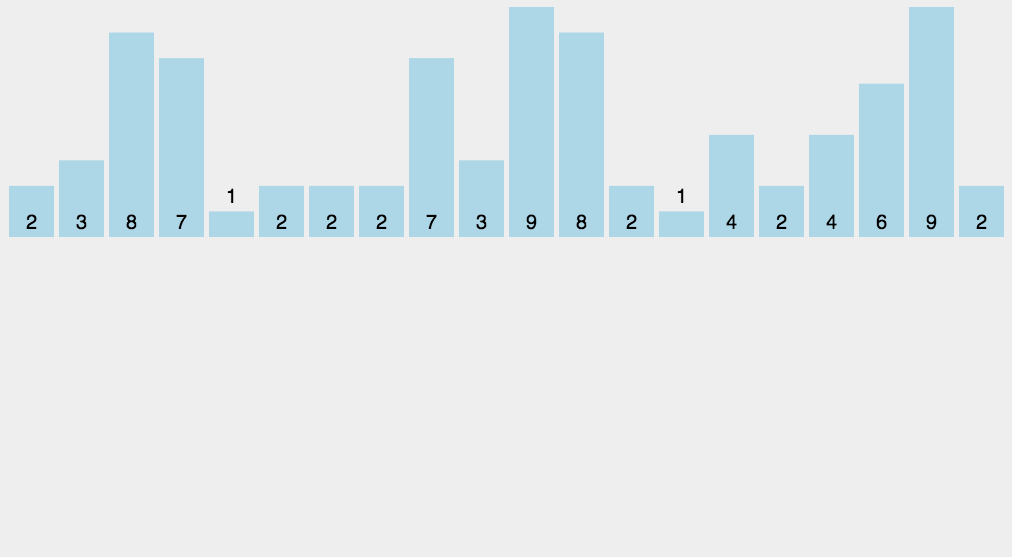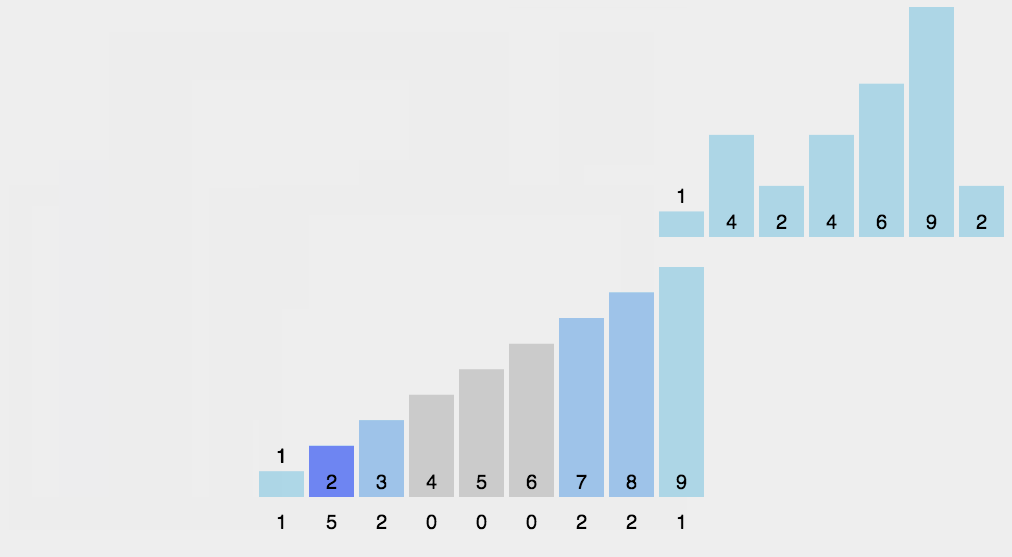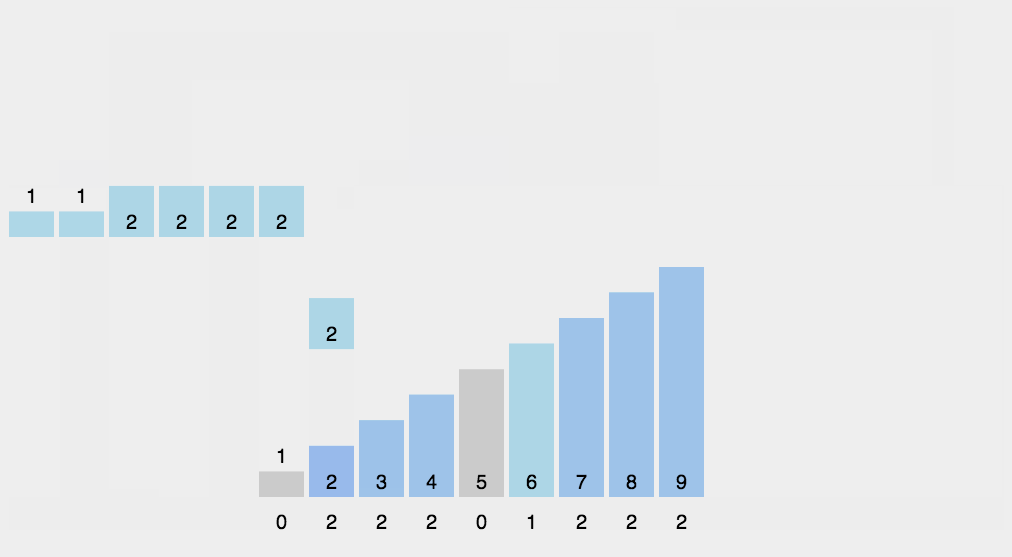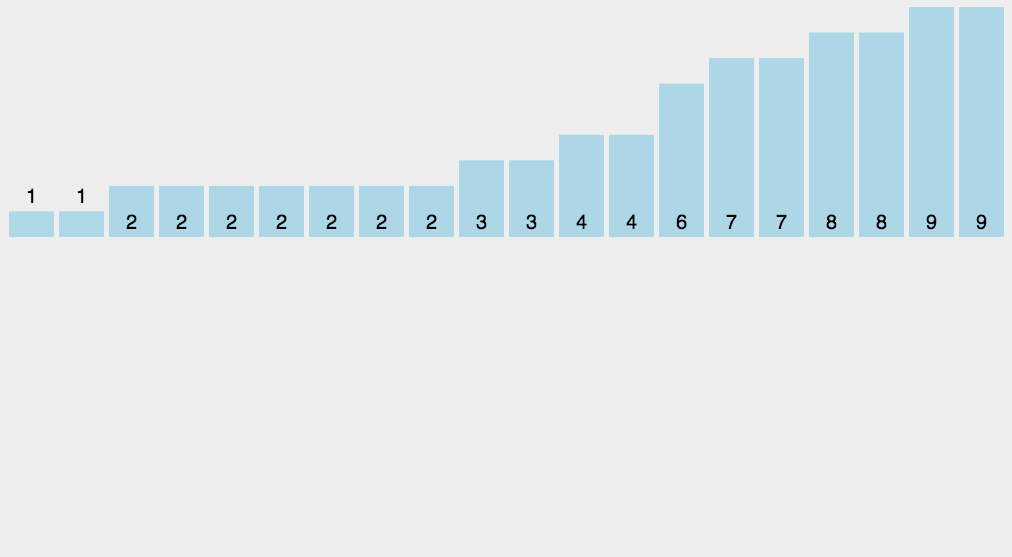
桶排序(Bucket Sort)的原理
将待排序数据分配到有限数量的桶里。每个桶再单独进行子排序,最后按顺序将多个桶中的数据进行合并,排序完成。当待排序的数组内的数值是均匀分配的时候,桶排序的时间复杂度为O(n)。
算法描述
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
public static void bucketSort(int[] arr){
//最大最小值
int max = arr[0];
int min = arr[0];
int length = arr.length;
for(int i=1; i<length; i++) {
if(arr[i] > max) {
max = arr[i];
} else if(arr[i] < min) {
min = arr[i];
}
}
//最大值和最小值的差
int diff = max - min;
//桶列表
ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();
for(int i = 0; i < length; i++){
bucketList.add(new ArrayList<>());
}
//每个桶的存数区间
float section = (float) diff / (float) (length - 1);
//数据入桶
for(int i = 0; i < length; i++){
//当前数除以区间得出存放桶的位置 减1后得出桶的下标
int num = (int) (arr[i] / section) - 1;
if(num < 0){
num = 0;
}
bucketList.get(num).add(arr[i]);
}
//桶内排序
for(int i = 0; i < bucketList.size(); i++){
//jdk的排序速度当然信得过
Collections.sort(bucketList.get(i));
}
//写入原数组
int index = 0;
for(ArrayList<Integer> arrayList : bucketList){
for(int value : arrayList){
arr[index] = value;
index++;
}
}
}动图演示

基数排序(Radix Sort)的原理
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
算法描述
- 取得数组中的最大数,并取得位数;
- array为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点)。
public class RadixSort {
public static int[] sort(int[] array,int maxDigit){
int[] result = new int[array.length];
//它的每一位的范围,0-9
int[] count = new int[10];
for(int i=0;i<maxDigit;i++){
int division = (int)Math.pow(10,i);
for(int n=0;n<array.length;n++){
//求每一位的数值,进行求余
int num = array[n]/division%10;
//将这个每一位的数值作为count的下标,再计算其出现多少次
count[num]++;
}
//进行累加,从下标值为1开始进行累加
for(int m=1;m<count.length;m++){
count[m] = count[m] + count[m-1];
}
//将原来的数组进行倒叙,通过累加后的count数组,
//获取count数组每个下标所对应的值就是下标的最后一个下标出现在result的位置减一,
//然后进行递减,这样做是稳定的,最后得到的数组的按顺序排列的
for(int j=array.length-1;j>=0;j--){
int num = array[j]/division%10;
result[--count[num]] = array[j];
}
//将array的数组里面的值复制为了result
System.arraycopy(result, 0, array, 0, array.length);
//填充count数组中的每个元素都是0,清空值
Arrays.fill(count,0);
}
return result;
}
//获取最高的位数
public static int getMaxDigit(int[] array){
int num=0;
//获取数组中最大的值
int maxValue = Arrays.stream(array).max().getAsInt();
//获取它的位数
while(maxValue!=0){
maxValue/=10;
num++;
}
return num;
}
public static void main(String[] args) {
int[] array = {312,236,187,330,222,457,113};
int[] result = sort(array,getMaxDigit(array));
System.out.println(Arrays.toString(result));
}
}动图演示

排序算法怎么选择
数据量规模较小,考虑直接插入或直接选择。当元素分布有序时直接插入将大大减少比较和移动记录的次数,如果不要求稳定性,可以使用直接选择,效率略高于直接插入。
数据量规模中等,选择希尔排序。
数据量规模较大,考虑堆排序(元素分布接近正序或逆序)、快速排序(元素分布随机)和归并排序(稳定性)。
一般不使用冒泡。